稳定边界层高度参数化方案的回归建模
为了发展一个适用于CAS-ESM气候系统模式的稳定边界层高度参数化方案,本研究基于湍流尺度分析理论,采用多元线性回归方法,对Zilitinkevich类型公式中的经验系数进行确定性拟合。该公式综合考虑了地表机械强迫、热力强迫以及自由大气静力稳定度的综合影响。
理论框架
我们所采用的参数化公式源于稳定层结下湍流动能的平衡关系,其函数形式如下:
11/h² = C1 * (f² / τ) + C2 * (N |f| / τ) + C3 * (|f β F₊| / τ²) 2
其中:
| 符号 | 含义 | 计算方式或来源 |
|---|---|---|
| h | 边界层高度 | 响应变量,来自ERA5 |
| τ | 表面摩擦速度 | τ = √(地表应力 / ρ),数据来自CAS-ESM |
| f | 科氏参数 | 由纬度计算得到 |
| N | 浮力频率 | N = √((g/θ) * ∂θ/∂z),由CAS-ESM位温廓线计算 |
| β | 热膨胀系数 | β = g / Ts,Ts为CAS-ESM地表温度 |
| F₊ | 湍流热通量尺度 | F₊ = SHFLX / (ρ Cp),SHFLX为CAS-ESM感热通量 |
| C1, C2, C3 | 待回归系数 | 本研究的目标 |
公式的物理意义:
- 第一项:机械湍流项 (
C1 f² / τ)
表征地表风应力产生的机械湍流与系统旋转(科氏力)效应之间的平衡。 - 第二项:稳定层结项 (
C2 N f / τ)
反映了自由大气层结稳定性(通过浮力频率N体现)对边界层发展的抑制。 - 第三项:热力强迫项 (
C3 f β F₊ / τ²)
描述了稳定层结下(通常F₊ < 0)地表负的热力强迫对湍流的削弱作用。
数据来源与预处理
本研究使用了两种数据源:
- 预测变量:来自 CAS-ESM 模式的历史模拟输出。
- 包括:地表应力、感热通量(
SHFLX)、地表温度、地表空气密度(ρ)、位温垂直廓线。 - 数据格式:2000年小时平均数据。
- 包括:地表应力、感热通量(
- 响应变量:作为回归目标的边界层高度数据,来自 ERA5再分析资料。
数据质量控制流程:
为了确保物理一致性并满足理论公式的适用条件,我们进行了严格的数据筛选:
- 稳定性筛选:仅选取稳定边界层情况下的数据点,核心判定标准为地表感热通量
H_s < 0(即向下)。 - 阈值筛选:为排除近中性边界林的干扰,设定了一个最小稳定度阈值,仅保留
(β F₊) / τ < -0.05的数据点。 - 重采样:所有数据均通过双线性插值重采样至共同网格(例如:1°×1°)。
- 时空范围:选取了 中高纬度大陆、海洋、中国南海区域。在2000年全年 的数据用于回归分析。
回归方法
将理论公式重构为一个关于因变量 1/h² 的多元线性回归模型:
1Y = C1 X1 + C2 X2 + C3 X3 2
其中:
Y = 1 / h_ERA5²X1 = f² / τX2 = N f / τX3 = f β F₊ / τ²
回归与验证细节:
- 算法:采用 普通最小二乘法 进行多元线性回归,以求解最优的系数组合
[C1, C2, C3]。 - 性能评估:回归模型的性能通过 决定系数 (R²) 进行评估。
- 稳健性验证:为验证模型的稳健性并避免过拟合,我们进一步进行了 k折交叉验证。
- 不确定性量化:计算了系数估计值的 95% 置信区间。
总结
通过这一严谨的数据驱动方法,我们得到了一个专为CAS-ESM模式优化的、物理意义明确的稳定边界层高度参数化方案。该方案将用于改进模式中边界层过程的物理表征,并对提升未来气候模拟的可靠性具有重要意义。
1import xarray as xr 2import numpy as np 3from sklearn.linear_model import LinearRegression 4from sklearn.metrics import r2_score 5import matplotlib.pyplot as plt 6 7 8# 读取数据 9ds1 = xr.open_dataset(r'CAS_ESM_factor.nc') # 包含TAUX,TAUY,SHFLX,n2,TS 10ds2 = xr.open_dataset(r'ERA5-2000-hour.nc') 11 12# 确保时间对齐 13print("检查时间对齐:") 14print("ds1时间:", ds1.time.values[:5]) 15print("ds2时间:", ds2.valid_time.values[:5]) 16 17#latindex = 91#北京 39 18#lonindex = 83#北京 19 20latindex = 78#南海 20N 21lonindex = 78#南海 110E 22 23latindex_ERA = 280 24lonindex_ERA = 440 25 26 27# 计算TAU = sqrt(TAUX^2 + TAUY^2) 28TAUX = ds1['TAUX'][:,latindex,lonindex] 29TAUY = ds1['TAUY'][:,latindex,lonindex] 30TAU = np.sqrt(TAUX**2 + TAUY**2) 31TS = ds1['TS'][:,latindex,lonindex] 32# 计算科里奥利参数f 33lat = ds1['lat'][latindex] 34f = 2 * 7.2921159e-5 * np.sin(np.deg2rad(20)) # 科里奥利参数 35 36# 获取观测的边界层高度 37blh_observed = ds2['blh'][:-24,latindex_ERA,lonindex_ERA] 38 39# 计算因变量 Y = 1/blh^2 40Y_valid = 1 / (blh_observed**2) 41 42# 准备自变量矩阵 X 43# 根据公式: 1/blh^2 = f^2/C1*TAU + N|f|/C2*TAU + f*SHFLX/C3*TAU^2 44# 重写为: 1/blh^2 = (f^2*TAU)/C1 + (N|f|*TAU)/C2 + (f*SHFLX)/(C3*TAU^2) 45# 令: X1 = f^2 * TAU, X2 = n2 * |f| * TAU, X3 = f * SHFLX / TAU^2 46 47# 注意:这里假设n2是Brunt-Väisälä频率,如果n2是其他参数请调整 48X1 = (f**2) / TAU 49 50X2 = np.sqrt(np.abs(ds1['n2'][:,0,latindex,lonindex])) * np.abs(f) / TAU 51 52X3 = f * ds1['SHFLX'][:,latindex,lonindex]*9.8/1005/1.2 / (TAU**2*TS) 53 54 55# 处理无穷大值(由于TAU可能接近0) 56#X3 = X3.where(np.isfinite(X3), 0) 57 58 59# 组合特征矩阵 60X_valid = np.column_stack([X1, X2, X3]) 61 62# 移除NaN和无穷大值 63#valid_mask = ~(np.isnan(Y_flat) | np.any(np.isnan(X_matrix), axis=1) | 64# np.any(np.isinf(X_matrix), axis=1)) 65#Y_valid = Y_flat[valid_mask] 66#X_valid = X_matrix[valid_mask] 67 68print(f"有效样本数: {len(Y_valid)}") 69 70# 执行多元线性回归 71reg = LinearRegression(fit_intercept=True) # 无截距项,因为公式中没有常数项 72reg.fit(X_valid, Y_valid) 73 74# 获取系数 75C1 = 1 / reg.coef_[0] 76C2 = 1 / reg.coef_[1] 77C3 = 1 / reg.coef_[2] 78 79# 预测值 80Y_pred = reg.predict(X_valid) 81 82# 计算统计指标 83r2 = r2_score(Y_valid, Y_pred) 84rmse = np.sqrt(np.mean((Y_valid - Y_pred)**2)) 85 86print("\n=== 回归结果 ===") 87print(f"C1 = {C1:.6f}") 88print(f"C2 = {C2:.6f}") 89print(f"C3 = {C3:.6f}") 90print(f"R² = {r2:.4f}") 91print(f"RMSE = {rmse:.6e}") 92print(f"系数: {reg.coef_}") 93#%% 94# 可视化诊断 95plt.figure(figsize=(15, 10)) 96 97# 1. 观测值 vs 预测值 98plt.subplot(2, 3, 1) 99plt.scatter(Y_valid, Y_pred, alpha=0.3, s=1) 100plt.plot([Y_valid.min(), Y_valid.max()], [Y_valid.min(), Y_valid.max()], 'r--') 101plt.xlabel('obs 1/BLH²') 102plt.ylabel('pred 1/BLH²') 103plt.title(f'obs vs pred (R² = {r2:.3f})') 104 105# 2. 残差图 106plt.subplot(2, 3, 2) 107residuals = Y_pred - Y_valid 108plt.scatter(Y_pred, residuals, alpha=0.3, s=1) 109plt.axhline(y=0, color='r', linestyle='--') 110plt.xlabel('pred') 111plt.ylabel('bias') 112plt.title('bias analysis') 113 114# 3. 各变量贡献 115plt.subplot(2, 3, 3) 116contributions = np.abs(reg.coef_ * np.mean(X_valid, axis=0)) 117labels = ['X1', 'X2', 'X3'] 118plt.pie(contributions, labels=labels, autopct='%1.1f%%') 119plt.title('') 120 121plt.tight_layout() 122plt.savefig('regression_diagnostics.png', dpi=300, bbox_inches='tight') 123plt.show() 124 125print(f"\n最终系数:") 126print(f"C1 = {C1:.6f}") 127print(f"C2 = {C2:.6f}") 128print(f"C3 = {C3:.6f}") 129
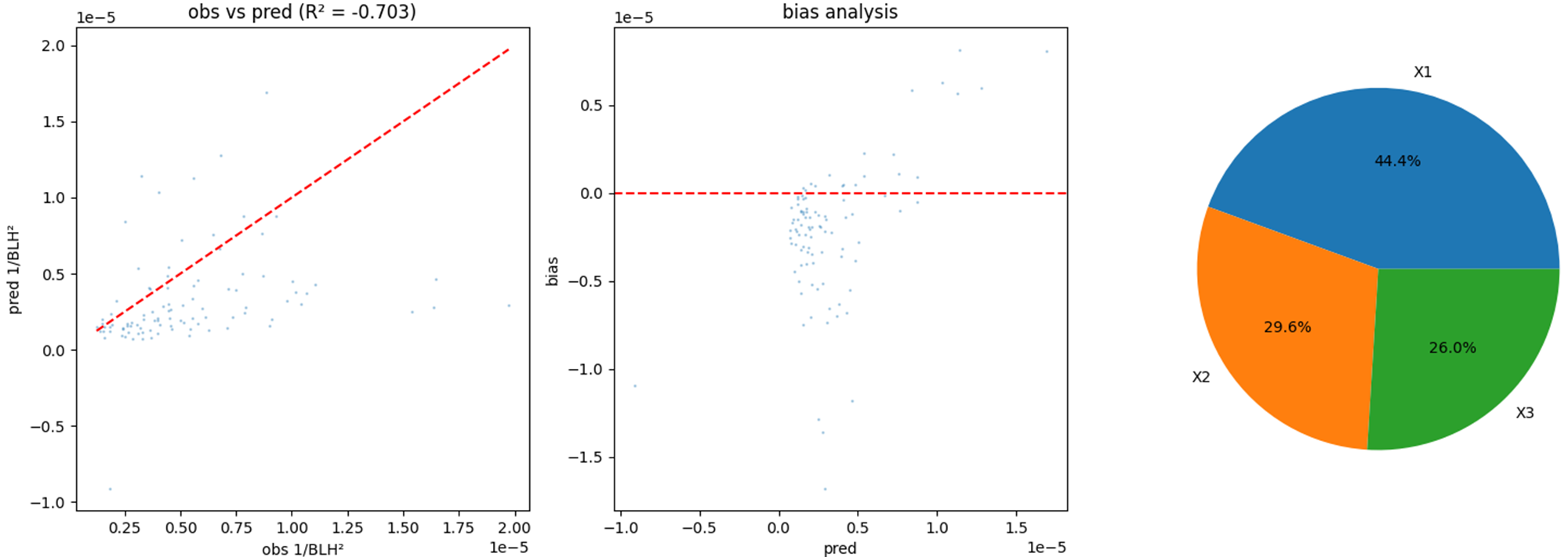
在南海附近,基本上都是稳定条件,很少能够用到稳定边界层高度公式,而利用南海附近的气象变量来回归稳定边界层高度公式本来就不可能得到很好的结果,因此我们应该把地区选在高纬度区域,季节选在北半球冬季。
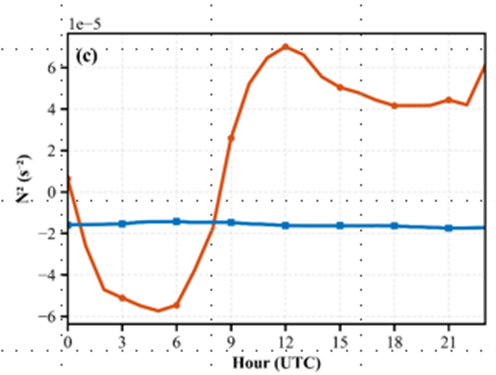
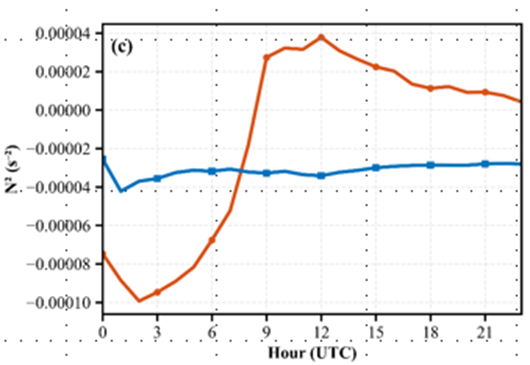
图分别是冬季和夏季一天的南海的浮力频率,都为不稳定状态,所以在南海上如果 采用最下面一层的稳定度来进行判断,则根本用不上稳定边界层高度,所以我们决定换高纬度冬季的数据再次尝试系数确定。
对每一天的边界层高度和影响因子进行线性拟合,能够在少量数据量情况下得到较好的模型。函数形式见图中黄色方框。
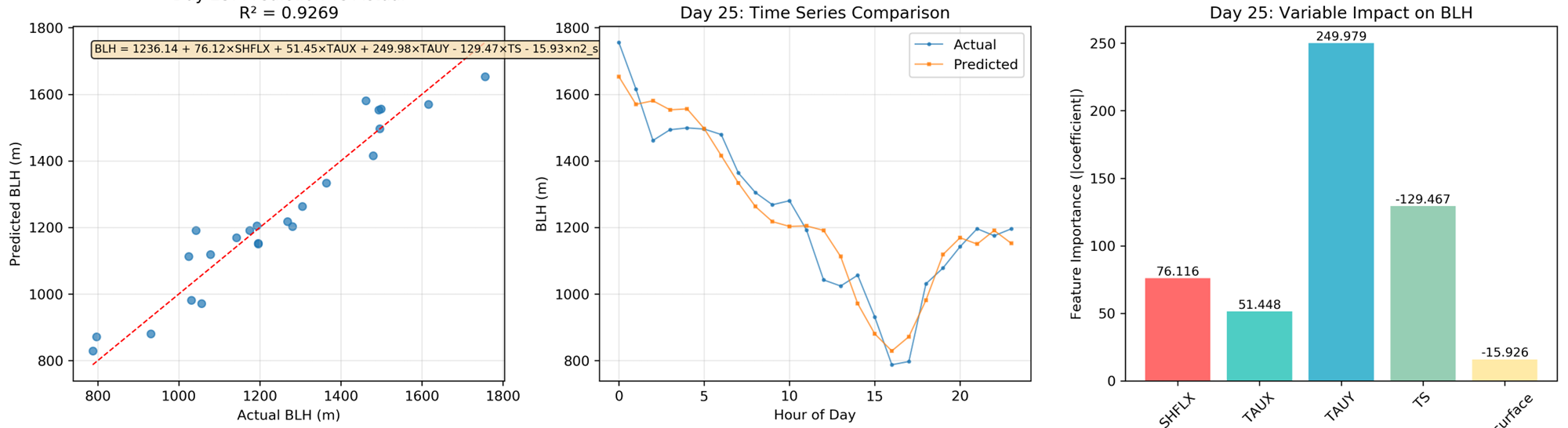
可是这种线性拟合的系数无法在长期保持一致性,比如在2000年1月的31天,每天的系数变动比较大,主要分成几种情况,这几种情况可能和每天的边界层稳定状况有关。
边界层高度的变化规律是非常复杂的,即使有这几种影响因子的描述,也无法在一个月时间尺度得到一个普适的线性诊断公式。
接着,我们考虑是因为不同稳定度情形导致边界层高度变化规律不同,我们将稳定条件(N>0)的因子和因变量挑出,进行拟合。如果对分别对365天 每天循环,从24小时挑出稳定条件样本进行特定函数形式拟合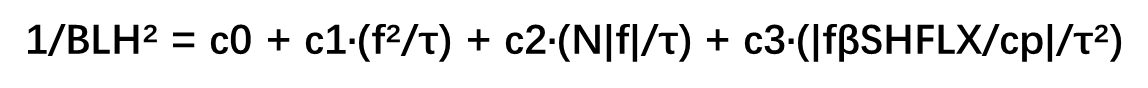
,能够得到每天的比较好的公式,可是同样普适性存在疑问。
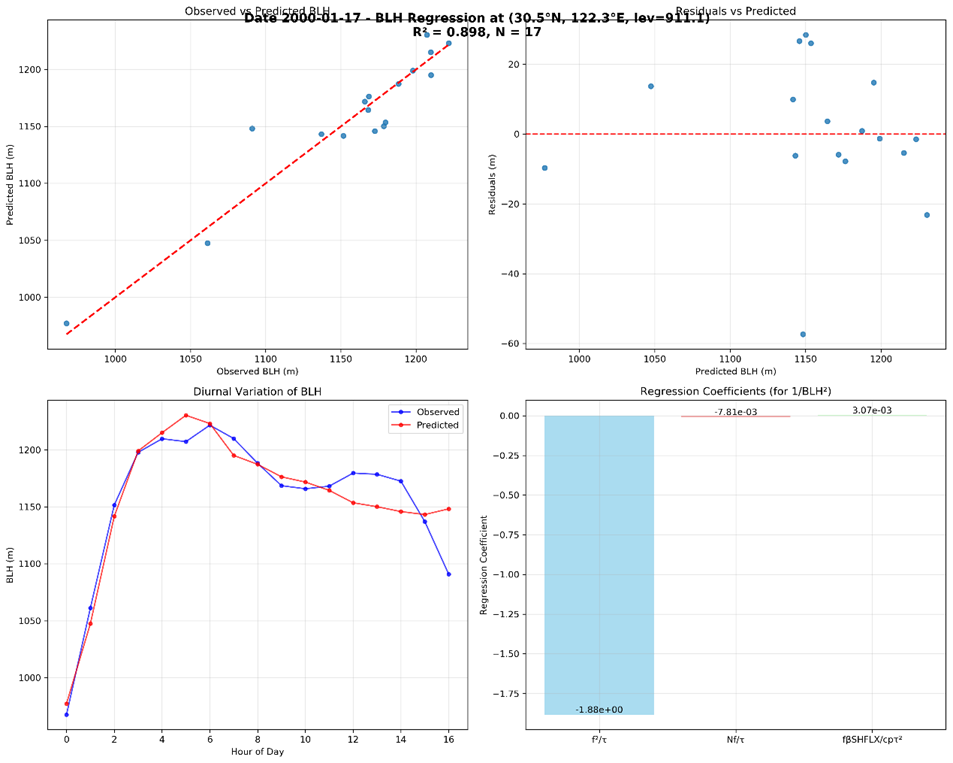
如下图,如果在一个月时间范围,决定系数降低到10%左右。
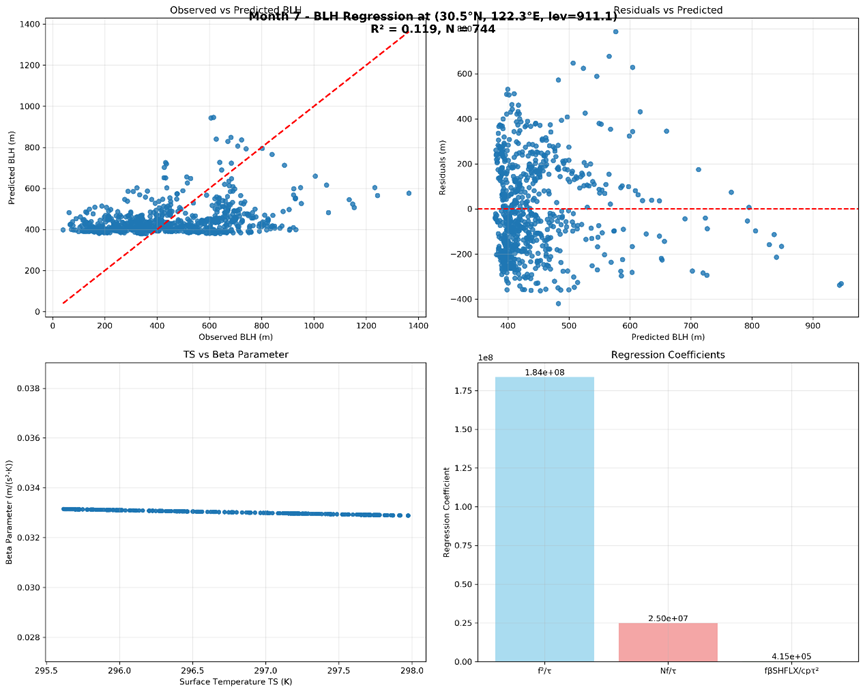
《稳定边界层高度参数化方案的回归建模》 是转载文章,点击查看原文。

