线性代数 - 叉积的分量形式与矩阵形式
flyfish
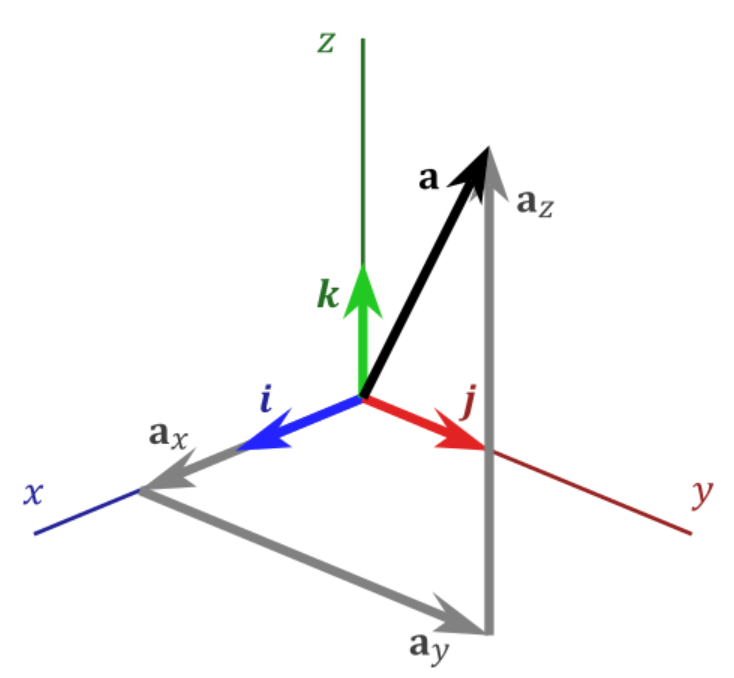
单位基向量与 向量的分解
1. 三维坐标系与单位基向量
图中蓝色的x轴、红色的y轴、绿色的z轴构成了一个右手系三维笛卡尔坐标系(符合“右手定则”的空间定向)。
在这个坐标系中,有三个单位基向量:
i^\hat{i}i^(蓝色箭头):沿x轴方向的单位向量;
j^\hat{j}j^(红色箭头):沿y轴方向的单位向量;
k^\hat{k}k^(绿色箭头):沿z轴方向的单位向量。
这三个基向量两两垂直(夹角为90∘90^\circ90∘)
2. 向量a⃗\vec{a}a的分量分解
黑色箭头表示的向量a⃗\vec{a}a可以分解为三个基向量方向上的分量:
axa_xax(灰色x方向箭头):a⃗\vec{a}a在x轴(i^\hat{i}i^方向)上的分量;
aya_yay(灰色y方向箭头):a⃗\vec{a}a在y轴(j^\hat{j}j^方向)上的分量;
aza_zaz(灰色z方向箭头):a⃗\vec{a}a在z轴(k^\hat{k}k^方向)上的分量。
从代数上,向量a⃗\vec{a}a可以表示为这三个分量与对应基向量的线性组合,类似三维空间里一个点需要用三个数来表示:
a⃗=axi^+ayj^+azk^ \vec{a} = a_x\hat{i} + a_y\hat{j} + a_z\hat{k}a=axi^+ayj^+azk^
叉积的分量形式
步骤1:明确基向量的叉积规则
三维空间的单位基向量 i^\hat{i}i^(x轴)、j^\hat{j}j^(y轴)、k^\hat{k}k^(z轴)仍满足以下性质:
- 自身叉乘为零:i^×i^=j^×j^=k^×k^=0\hat{i} \times \hat{i} = \hat{j} \times \hat{j} = \hat{k} \times \hat{k} = 0i^×i^=j^×j^=k^×k^=0;
- 循环正方向(右手定则):i^×j^=k^\hat{i} \times \hat{j} = \hat{k}i^×j^=k^,j^×k^=i^\hat{j} \times \hat{k} = \hat{i}j^×k^=i^,k^×i^=j^\hat{k} \times \hat{i} = \hat{j}k^×i^=j^;
- 交换顺序变号:j^×i^=−k^\hat{j} \times \hat{i} = -\hat{k}j^×i^=−k^,k^×j^=−i^\hat{k} \times \hat{j} = -\hat{i}k^×j^=−i^,i^×k^=−j^\hat{i} \times \hat{k} = -\hat{j}i^×k^=−j^。
步骤2:将向量 a⃗\vec{a}a 和 b⃗\vec{b}b 用基向量展开
设小写向量 a⃗\vec{a}a 沿x、y、z轴的分量为 ax,ay,aza_x, a_y, a_zax,ay,az,b⃗\vec{b}b 的分量为 bx,by,bzb_x, b_y, b_zbx,by,bz,则:
a⃗=axi^+ayj^+azk^,b⃗=bxi^+byj^+bzk^ \vec{a} = a_x\hat{i} + a_y\hat{j} + a_z\hat{k}, \quad \vec{b} = b_x\hat{i} + b_y\hat{j} + b_z\hat{k}a=axi^+ayj^+azk^,b=bxi^+byj^+bzk^
步骤3:利用叉积的分配律展开 a⃗×b⃗\vec{a} \times \vec{b}a×b
按分配律将两个向量的基向量形式逐项叉乘(共9项):
a⃗×b⃗=(axi^+ayj^+azk^)×(bxi^+byj^+bzk^)=axi^×bxi^+axi^×byj^+axi^×bzk^+ayj^×bxi^+ayj^×byj^+ayj^×bzk^+azk^×bxi^+azk^×byj^+azk^×bzk^. \begin{align*} \vec{a} \times \vec{b} &= (a_x\hat{i} + a_y\hat{j} + a_z\hat{k}) \times (b_x\hat{i} + b_y\hat{j} + b_z\hat{k}) \\ &= a_x\hat{i} \times b_x\hat{i} + a_x\hat{i} \times b_y\hat{j} + a_x\hat{i} \times b_z\hat{k} \\ &\quad + a_y\hat{j} \times b_x\hat{i} + a_y\hat{j} \times b_y\hat{j} + a_y\hat{j} \times b_z\hat{k} \\ &\quad + a_z\hat{k} \times b_x\hat{i} + a_z\hat{k} \times b_y\hat{j} + a_z\hat{k} \times b_z\hat{k}. \end{align*}a×b=(axi^+ayj^+azk^)×(bxi^+byj^+bzk^)=axi^×bxi^+axi^×byj^+axi^×bzk^+ayj^×bxi^+ayj^×byj^+ayj^×bzk^+azk^×bxi^+azk^×byj^+azk^×bzk^.
步骤4:利用基向量规则化简每一项
对9项分别应用步骤1的规则,消去零项并整理符号:
- axbxi^×i^=0a_xb_x\hat{i} \times \hat{i} = 0axbxi^×i^=0(自身叉乘为零);
- axbyi^×j^=axby⋅k^a_xb_y\hat{i} \times \hat{j} = a_xb_y \cdot \hat{k}axbyi^×j^=axby⋅k^(循环正方向);
- axbzi^×k^=axbz⋅(−j^)a_xb_z\hat{i} \times \hat{k} = a_xb_z \cdot (-\hat{j})axbzi^×k^=axbz⋅(−j^)(交换顺序变号);
- aybxj^×i^=aybx⋅(−k^)a_yb_x\hat{j} \times \hat{i} = a_yb_x \cdot (-\hat{k})aybxj^×i^=aybx⋅(−k^)(交换顺序变号);
- aybyj^×j^=0a_yb_y\hat{j} \times \hat{j} = 0aybyj^×j^=0(自身叉乘为零);
- aybzj^×k^=aybz⋅i^a_yb_z\hat{j} \times \hat{k} = a_yb_z \cdot \hat{i}aybzj^×k^=aybz⋅i^(循环正方向);
- azbxk^×i^=azbx⋅j^a_zb_x\hat{k} \times \hat{i} = a_zb_x \cdot \hat{j}azbxk^×i^=azbx⋅j^(循环正方向);
- azbyk^×j^=azby⋅(−i^)a_zb_y\hat{k} \times \hat{j} = a_zb_y \cdot (-\hat{i})azbyk^×j^=azby⋅(−i^)(交换顺序变号);
- azbzk^×k^=0a_zb_z\hat{k} \times \hat{k} = 0azbzk^×k^=0(自身叉乘为零)。
步骤5:合并同类基向量的项
按 i^\hat{i}i^(x轴)、j^\hat{j}j^(y轴)、k^\hat{k}k^(z轴)分类,合并同一方向的非零项:
- i^\hat{i}i^ 方向:项6 + 项8 = aybzi^−azbyi^=(aybz−azby)i^a_yb_z\hat{i} - a_zb_y\hat{i} = (a_yb_z - a_zb_y)\hat{i}aybzi^−azbyi^=(aybz−azby)i^;
- j^\hat{j}j^ 方向:项3 + 项7 = −axbzj^+azbxj^=(azbx−axbz)j^-a_xb_z\hat{j} + a_zb_x\hat{j} = (a_zb_x - a_xb_z)\hat{j}−axbzj^+azbxj^=(azbx−axbz)j^;
- k^\hat{k}k^ 方向:项2 + 项4 = axbyk^−aybxk^=(axby−aybx)k^a_xb_y\hat{k} - a_yb_x\hat{k} = (a_xb_y - a_yb_x)\hat{k}axbyk^−aybxk^=(axby−aybx)k^。
最终结果
a⃗×b⃗=(aybz−azby)i^+(azbx−axbz)j^+(axby−aybx)k^ \vec{a} \times \vec{b} = \boxed{(a_yb_z - a_zb_y)\hat{i} + (a_zb_x - a_xb_z)\hat{j} + (a_xb_y - a_yb_x)\hat{k}}a×b=(aybz−azby)i^+(azbx−axbz)j^+(axby−aybx)k^
叉积的矩阵形式(三阶行列式)
叉积 a⃗×b⃗\vec{a} \times \vec{b}a×b 最标准的矩阵表示的是 以基向量为第一行、a⃗\vec{a}a 分量为第二行、b⃗\vec{b}b 分量为第三行的三阶行列式,矩阵结构与图中坐标系(i^\hat{i}i^-x轴、j^\hat{j}j^-y轴、k^\hat{k}k^-z轴)完全对应:
a⃗×b⃗=∣i^j^k^axayazbxbybz∣ \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}a×b=i^axbxj^aybyk^azbz
矩阵中各元素的含义:
第一行:i^,j^,k^\hat{i}, \hat{j}, \hat{k}i^,j^,k^(x、y、z轴的单位基向量,蓝色、红色、绿色箭头);
第二行:ax,ay,aza_x, a_y, a_zax,ay,az(向量 a⃗\vec{a}a 沿x、y、z轴的分量);
第三行:bx,by,bzb_x, b_y, b_zbx,by,bz(向量 b⃗\vec{b}b 沿x、y、z轴的分量)。
矩阵(行列式)展开与分量形式的关联
这个三阶行列式按 第一行(基向量行)展开,就得到之前叉积分量形式,衔接矩阵运算与代数表达式:
∣i^j^k^axayazbxbybz∣=i^⋅∣ayazbybz∣−j^⋅∣axazbxbz∣+k^⋅∣axaybxby∣ \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix} = \hat{i} \cdot \begin{vmatrix} a_y & a_z \\ b_y & b_z \end{vmatrix} - \hat{j} \cdot \begin{vmatrix} a_x & a_z \\ b_x & b_z \end{vmatrix} + \hat{k} \cdot \begin{vmatrix} a_x & a_y \\ b_x & b_y \end{vmatrix}i^axbxj^aybyk^azbz=i^⋅aybyazbz−j^⋅axbxazbz+k^⋅axbxayby
再计算每个二阶行列式(主对角线减副对角线):
∣ayazbybz∣=aybz−azby\begin{vmatrix} a_y & a_z \\ b_y & b_z \end{vmatrix} = a_y b_z - a_z b_yaybyazbz=aybz−azby(i^\hat{i}i^ 方向分量);
∣axazbxbz∣=axbz−azbx\begin{vmatrix} a_x & a_z \\ b_x & b_z \end{vmatrix} = a_x b_z - a_z b_xaxbxazbz=axbz−azbx(乘以负号后为 j^\hat{j}j^ 方向分量);
∣axaybxby∣=axby−aybx\begin{vmatrix} a_x & a_y \\ b_x & b_y \end{vmatrix} = a_x b_y - a_y b_xaxbxayby=axby−aybx(k^\hat{k}k^ 方向分量)。
最终结果和之前一致,矩阵形式是叉积的“紧凑表达”,展开后就是具体分量:
a⃗×b⃗=(aybz−azby)i^+(azbx−axbz)j^+(axby−aybx)k^ \vec{a} \times \vec{b} = (a_y b_z - a_z b_y)\hat{i} + (a_z b_x - a_x b_z)\hat{j} + (a_x b_y - a_y b_x)\hat{k}a×b=(aybz−azby)i^+(azbx−axbz)j^+(axby−aybx)k^
《线性代数 - 叉积的分量形式与矩阵形式》 是转载文章,点击查看原文。
