对于刚入门机器学习的同学来说,“高维数据” 是很容易遇到的痛点 —— 比如处理包含几十甚至上百个特征的数据集时,不仅训练速度变慢,模型还可能因为 “维度太多” 出现泛化能力下降的问题。而 “降维” 正是解决高维数据困境的核心技术。今天我们就从基础概念出发,拆解 “维度灾难” 的危害、降维的本质,以及经典的低维嵌入方法,帮你彻底理解降维为什么重要、到底在做什么。
一、先搞懂:什么是 “维度”?为什么会有 “维度灾难”?
在学习降维前,我们需要先明确 “维度” 的定义,以及高维数据会带来的核心问题 ——“维度灾难”(curse of dimensionality)。这是理解降维意义的前提。
1. 维度:数据特征的 “数量”
在机器学习中,“维度” 通常指数据的特征数量。比如:
- 用 “色泽、根蒂、敲声”3 个特征判断好瓜,这就是 3 维数据;
- 用 “身高、体重、年龄、血压、血糖”5 个特征预测健康状况,这就是 5 维数据;
- 如果特征数量增加到 100 个,那就是 100 维数据,也就是我们说的 “高维数据”。
每个特征就像数据的 “一个观察角度”,维度越高,观察角度越细,但也会带来新的问题。
2. 维度灾难:高维数据的 “致命痛点”
“维度灾难” 指当数据维度不断增加时,数据在空间中的分布会变得越来越稀疏,导致传统的数据分析方法(如距离计算、邻域搜索)失效,最终影响模型性能。我们可以从两个最直观的角度理解它:
(1)欧式距离的 “失效”:高维空间中距离失去区分度
在低维空间中,我们常用 “欧式距离” 衡量两个样本的相似性 —— 距离越近,相似性越高。比如:
- 二维空间(如 x-y 平面):两个点(x1,y1)和(x2,y2)的欧式距离公式为:ρ=(x2−x1)2+(y2−y1)2比如点 (1,2) 和 (3,4) 的距离是(3−1)2+(4−2)2=8≈2.83,距离大小能直观反映相似性。
- 三维空间(如 x-y-z 立体空间):距离公式扩展为:ρ=(x2−x1)2+(y2−y1)2+(z2−z1)2虽然计算稍复杂,但距离仍有明确的区分度。
- n 维空间(高维):距离公式进一步扩展为:d(x,y)=∑i=1n(xi−yi)2
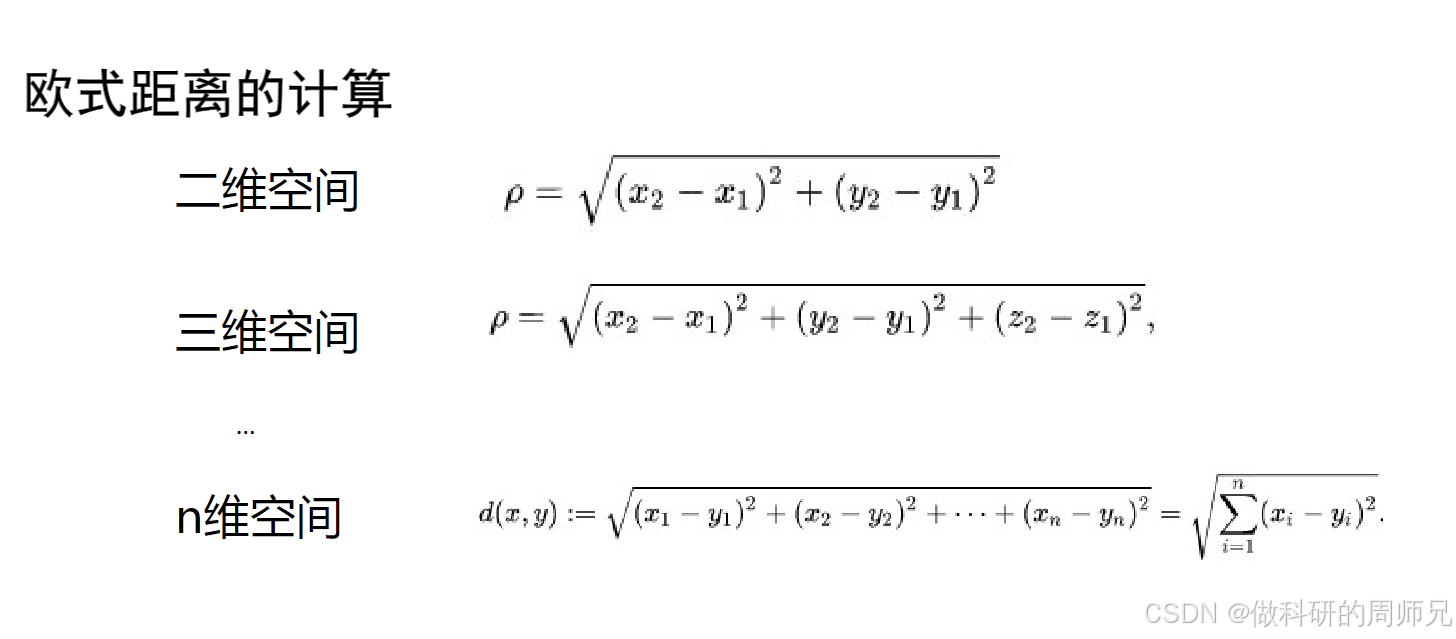
图片来源于网络,仅供学习参考
图片来源于网络,仅供学习参考
问题来了:当维度 n 不断增大时,所有样本之间的欧式距离会逐渐趋近于相等。比如在 1000 维空间中,两个随机样本的距离可能都在某个固定范围(如 10~12)内,此时 “距离近 = 相似” 的逻辑完全失效 —— 模型无法通过距离判断样本是否相似,像 KNN 这类依赖距离的算法会直接 “失灵”。
(2)数据稀疏性:高维空间中 “样本不够用”
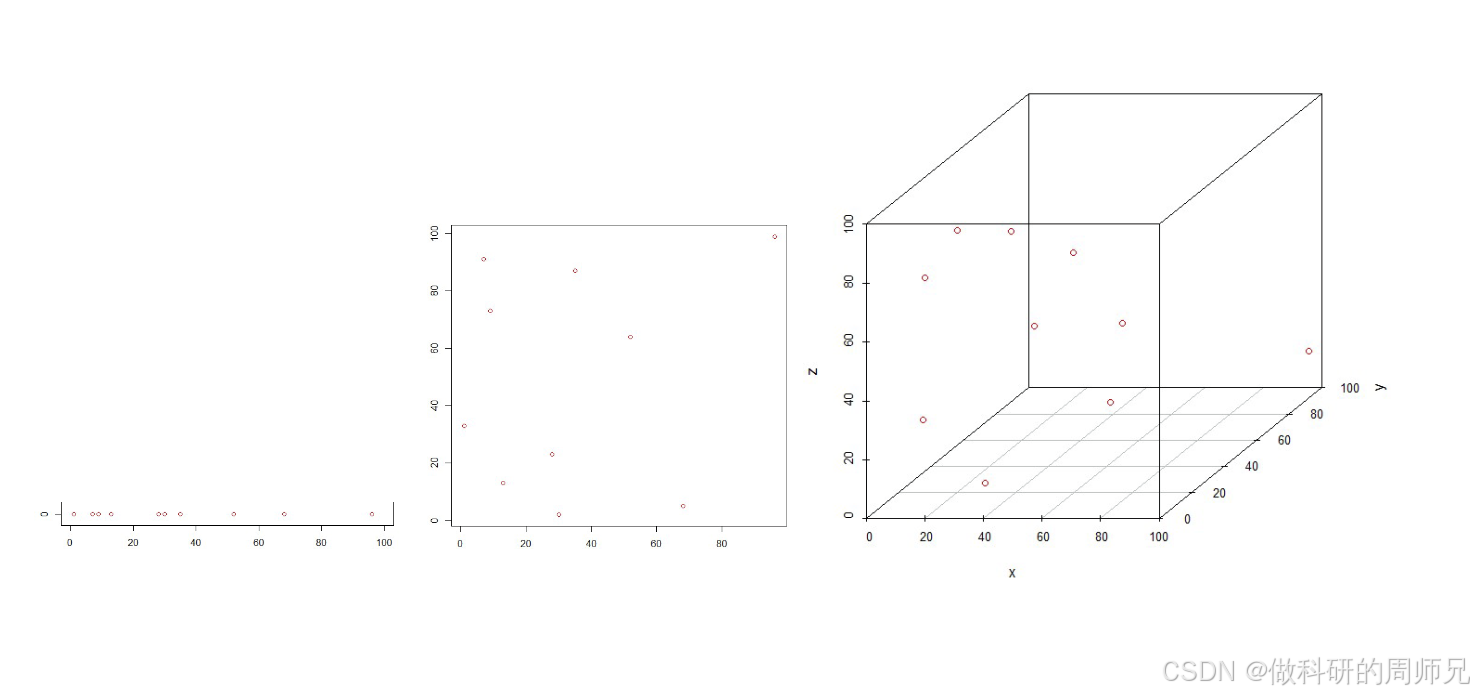
想象一个简单场景:我们要在空间中均匀采样,保证每个 “小区域” 都有样本覆盖。
- 二维空间:如果特征范围是 [0,100],把每个维度分成 10 段,会得到 10×10=100 个小区域,100 个样本就能基本覆盖;
- 三维空间:同样分成 10 段,会得到 10×10×10=1000 个小区域,需要 1000 个样本才能覆盖;
- 10 维空间:会得到1010个小区域,哪怕有 100 万样本,也只能覆盖10−4(万分之一)的区域。
这就是高维数据的稀疏性 —— 维度越高,要覆盖空间所需的样本量呈指数级增长。而现实中我们的样本量往往有限,高维空间中大部分区域都是 “空的”,模型只能在稀疏的样本上学习,很容易出现过拟合,泛化能力大幅下降。
(3)计算成本飙升:高维数据 “拖慢” 模型训练
维度越高,数据的存储和计算成本也会显著增加。比如:
- 存储 1 个 1000 维的样本,需要 1000 个数值;存储 10 万条这样的样本,就是 1 亿个数值,对内存压力很大;
- 模型训练时(如线性回归、决策树),需要遍历每个特征进行计算,维度越多,训练时间越长 ——1000 维数据的训练时间可能是 10 维数据的几十倍。
二、降维的本质:“压缩数据” 但不丢失关键信息
既然高维数据有这么多问题,那 “降维” 是不是简单地 “删掉一些特征”?当然不是。
1. 降维的定义:从 “高维空间” 到 “低维空间” 的映射
降维的核心是将高维数据(d 维)通过某种数学变换,映射到低维空间(d' 维,d' < d),同时尽可能保留原始数据中的 “关键信息”(如样本的相似性、结构关系)。
举个形象的例子:我们用 “长、宽、高”3 个特征描述一个长方体(3 维数据),但如果我们只关心它的 “占地面积”,可以用 “长 × 宽” 得到面积(1 维数据)—— 这就是一种简单的降维:从 3 维压缩到 1 维,同时保留了 “占地面积” 这个关键信息,丢掉了 “高度” 这个次要信息。
再比如:处理人脸图像时,一张 256×256 的灰度图有 65536 个像素(65536 维数据),但人脸的关键特征(如眼睛位置、鼻子形状、脸型)其实可以用几十个维度表示 —— 降维就是把 65536 维的像素数据,压缩到几十维的 “特征向量”,既减少了维度,又保留了识别人脸的关键信息。
2. 降维的核心目标:解决维度灾难,提升模型效率
降维的最终目的是 “扬长避短”:
- 避短:降低数据维度,解决维度灾难带来的距离失效、数据稀疏、计算成本高的问题;
- 扬长:保留原始数据的关键信息,确保降维后的数据仍能用于后续的模型训练(如分类、回归),且模型性能不会大幅下降。
简单来说,降维就是 “给数据减肥”—— 去掉冗余的 “脂肪”(无用或重复的特征),保留关键的 “肌肉”(核心信息)。
三、经典降维思路:低维嵌入与多维缩放(MDS)
降维有很多具体算法,比如 PCA(主成分分析)、t-SNE、LDA 等,而 “多维缩放(Multiple Dimensional Scaling,MDS)” 是最直观的低维嵌入算法之一,能帮我们理解降维的核心逻辑 ——保持样本间的距离关系。
1. 低维嵌入:让降维后的数据 “还原” 原始结构
“低维嵌入” 是很多降维算法的核心思路,指的是:将高维空间中的样本,“嵌入” 到低维空间中,使得样本在低维空间中的 “结构关系”(如距离、邻域)与高维空间中尽可能一致。
比如高维空间中两个样本距离很近,嵌入到低维空间后,它们的距离也应该很近;高维空间中两个样本距离很远,低维空间中距离也应该很远 —— 这就是 MDS 算法的核心目标。
图片来源于网络,仅供学习参考
2. MDS 算法的核心步骤:从 “距离矩阵” 到 “低维坐标”
MDS 的思路很清晰:不直接处理原始特征,而是基于样本间的 “距离矩阵”,找到低维空间中的坐标,让低维空间的距离与原始距离尽可能一致。具体步骤可以拆解为 3 步:
步骤 1:计算原始高维空间的距离矩阵 D
假设有 m 个样本,每个样本是 d 维数据。首先计算任意两个样本之间的距离(如欧式距离),得到一个 m×m 的距离矩阵 D。矩阵中第 i 行第 j 列的元素distij,表示第 i 个样本和第 j 个样本在高维空间中的距离。
比如有 3 个样本 A、B、C,距离矩阵 D 可能是:
| A | B | C | |
|---|---|---|---|
| A | 0 | 2 | 5 |
| B | 2 | 0 | 4 |
| C | 5 | 4 | 0 |
| 表示 A 和 B 距离 2,A 和 C 距离 5,B 和 C 距离 4。 |
步骤 2:定义低维空间的目标 —— 保持距离一致
MDS 的目标是找到一个 d' 维(d' < d)的低维空间,让每个样本在低维空间中有一个坐标表示(记为zi,zi是 d' 维向量),且任意两个样本在低维空间的欧式距离,等于原始高维空间的距离,即:∥zi−zj∥=distij
其中∥zi−zj∥表示低维空间中样本 i 和 j 的欧式距离。

图片来源于网络,仅供学习参考
步骤 3:通过数学变换求解低维坐标 Z
为了找到满足条件的低维坐标,MDS 引入了 “内积矩阵 B” 的概念:
- 设低维坐标矩阵为 Z(d'×m,每一列是一个样本的低维坐标),则内积矩阵 B = ZᵀZ(m×m),矩阵中第 i 行第 j 列的元素bij=ziTzj(样本 i 和 j 低维坐标的内积)。
- 根据欧式距离的数学性质,原始距离distij2和内积bij有如下关系:distij2=∥zi∥2+∥zj∥2−2bij其中∥zi∥2=ziTzi=bii(样本 i 低维坐标的模长平方,即内积矩阵 B 的对角线元素)。
通过这个公式,我们可以从已知的距离矩阵 D,推导出内积矩阵 B;再对 B 进行矩阵分解(如特征值分解),就能得到低维坐标矩阵 Z—— 这样就完成了从高维到低维的映射,且保证了样本间的距离关系尽可能不变。
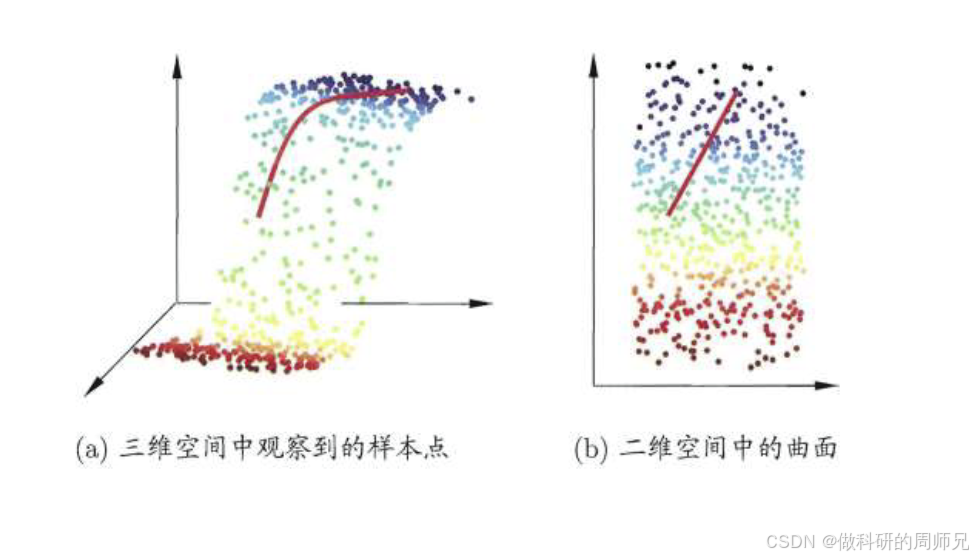
3. MDS 的直观例子:3 维数据嵌入到 2 维
比如我们有一组 3 维空间中的样本(比如一个曲面上的点),直接观察 3 维数据很困难。通过 MDS 将其嵌入到 2 维空间后,我们可以在平面上直观地看到样本的分布结构 —— 比如哪些样本聚在一起,哪些样本离得远,而这种结构与 3 维空间中完全一致。这就是低维嵌入的价值:将高维数据 “压扁” 到低维,既保留了核心结构,又方便可视化和后续分析。
四、入门总结与降维的应用场景
- 核心逻辑回顾:降维是为了解决 “维度灾难”,通过数学变换将高维数据映射到低维空间,同时保留关键信息(如距离、结构),最终提升模型效率和泛化能力。
- 关键概念区分:
- 维度灾难:高维数据导致的距离失效、数据稀疏、计算成本高的问题;
- 低维嵌入:降维的核心思路,保持样本在低维空间的结构与高维空间一致;
- MDS:经典的低维嵌入算法,基于距离矩阵求解低维坐标,保证距离不变。
- 常见应用场景:
- 数据可视化:将高维数据(如 100 维)降维到 2 维或 3 维,用散点图直观展示样本分布;
- 模型优化:预处理高维数据(如图片、文本),降低维度后再训练模型(如 KNN、SVM),减少计算成本,避免过拟合;
- 特征压缩:将冗余的多特征压缩为少数核心特征,简化模型解释(如用 “综合健康指数” 替代多个健康指标)。
对于刚入门的同学,不需要一开始就深入 MDS 的数学推导,重点是理解 “维度灾难的危害” 和 “降维的核心目标”。后续我们会讲解更常用的降维算法(如 PCA)和具体代码实践,帮你真正掌握降维的应用。
MDS 算法 Python 实践代码模板(高维数据降维与可视化)
以下代码基于scikit-learn和matplotlib实现 MDS(多维缩放)算法,包含高维数据生成、MDS 降维、降维前后距离一致性验证及结果可视化,全程贴合 “降维保留关键结构” 的核心逻辑,可直接复制到 CSDN 推文的实践部分,帮助入门学生直观感受降维效果。
一、环境依赖
首先确保安装所需 Python 库,未安装则执行以下命令:
1pip install numpy pandas scikit-learn matplotlib 2
二、完整代码实现
1. 导入所需库
1import numpy as np 2import matplotlib.pyplot as plt 3from sklearn.manifold import MDS 4from sklearn.metrics import pairwise_distances 5from mpl_toolkits.mplot3d import Axes3D # 用于3D数据可视化 6
2. 生成高维测试数据(模拟真实高维结构)
为了直观体现 MDS “保留距离结构” 的效果,我们先生成一组3 维空间中带明显结构的数据(如 3 个聚类的点),再用 MDS 将其降维到 2 维,观察结构是否保留:
1# 设置随机种子,保证结果可复现 2np.random.seed(42) 3 4# 生成3维空间中的3个聚类(每个聚类50个样本,共150个样本) 5# 聚类1:中心(0, 0, 0),标准差0.5 6cluster1 = np.random.normal(loc=[0, 0, 0], scale=0.5, size=(50, 3)) 7# 聚类2:中心(5, 5, 5),标准差0.5(与聚类1距离较远) 8cluster2 = np.random.normal(loc=[5, 5, 5], scale=0.5, size=(50, 3)) 9# 聚类3:中心(5, 0, 5),标准差0.5(与聚类1、2距离适中) 10cluster3 = np.random.normal(loc=[5, 0, 5], scale=0.5, size=(50, 3)) 11 12# 合并为3维高维数据集(150个样本,3个特征) 13high_dim_data = np.vstack([cluster1, cluster2, cluster3]) 14# 生成标签(用于可视化区分聚类):0=聚类1,1=聚类2,2=聚类3 15labels = np.array([0]*50 + [1]*50 + [2]*50) 16 17# 查看高维数据基本信息 18print(f"高维数据形状:{high_dim_data.shape}(样本数:{high_dim_data.shape[0]},维度:{high_dim_data.shape[1]})") 19print(f"标签分布:聚类1={sum(labels==0)}个,聚类2={sum(labels==1)}个,聚类3={sum(labels==2)}个") 20 21# 计算高维空间中样本的距离矩阵(欧式距离) 22high_dim_dist = pairwise_distances(high_dim_data, metric='euclidean') 23print(f"高维距离矩阵形状:{high_dim_dist.shape}(150×150,每个元素为对应样本对的欧式距离)") 24
3. MDS 降维(3 维→2 维)
使用sklearn的MDS类实现降维,核心参数n_components设置为 2(目标低维维度),并通过dissimilarity='precomputed'指定使用预计算的距离矩阵(也可直接传入高维数据,由 MDS 自动计算距离):
1# 初始化MDS模型(目标降维到2维,保留距离结构) 2mds = MDS( 3 n_components=2, # 降维后的维度(核心参数) 4 dissimilarity='precomputed', # 输入为预计算的距离矩阵 5 random_state=42, # 随机种子,保证结果可复现 6 n_init=10 # 多次初始化,选择最优结果(避免局部最优) 7) 8 9# 执行MDS降维:输入高维距离矩阵,输出2维低维数据 10low_dim_data = mds.fit_transform(high_dim_dist) 11 12# 查看降维后数据信息 13print(f"\nMDS降维后数据形状:{low_dim_data.shape}(样本数:{low_dim_data.shape[0]},维度:{low_dim_data.shape[1]})") 14 15# 计算低维空间中样本的距离矩阵(验证距离是否保留) 16low_dim_dist = pairwise_distances(low_dim_data, metric='euclidean') 17 18# 验证降维前后的距离一致性(计算距离矩阵的相关系数,越接近1说明一致性越好) 19distance_corr = np.corrcoef(high_dim_dist.flatten(), low_dim_dist.flatten())[0, 1] 20print(f"高维与低维距离矩阵的相关系数:{distance_corr:.4f}(接近1表示距离结构保留良好)") 21
4. 结果可视化(高维数据 vs 低维数据)
通过 3D 图展示原始高维数据的结构,2D 图展示 MDS 降维后的结构,直观对比 “聚类结构是否保留”:
1# 设置中文字体(避免matplotlib中文乱码) 2plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans'] 3plt.rcParams['axes.unicode_minus'] = False 4 5# 创建画布(1行2列,左侧3D高维图,右侧2D低维图) 6fig = plt.figure(figsize=(15, 6)) 7 8# 1. 绘制原始3维高维数据(左侧子图) 9ax1 = fig.add_subplot(121, projection='3d') 10# 分别绘制3个聚类(用不同颜色和标记区分) 11scatter1 = ax1.scatter( 12 high_dim_data[labels==0, 0], high_dim_data[labels==0, 1], high_dim_data[labels==0, 2], 13 c='red', marker='o', s=50, label='聚类1', alpha=0.7 14) 15scatter2 = ax1.scatter( 16 high_dim_data[labels==1, 0], high_dim_data[labels==1, 1], high_dim_data[labels==1, 2], 17 c='blue', marker='s', s=50, label='聚类2', alpha=0.7 18) 19scatter3 = ax1.scatter( 20 high_dim_data[labels==2, 0], high_dim_data[labels==2, 1], high_dim_data[labels==2, 2], 21 c='green', marker='^', s=50, label='聚类3', alpha=0.7 22) 23# 设置3D图标签和标题 24ax1.set_xlabel('3维特征1', fontsize=12) 25ax1.set_ylabel('3维特征2', fontsize=12) 26ax1.set_zlabel('3维特征3', fontsize=12) 27ax1.set_title('原始3维高维数据结构', fontsize=14, pad=20) 28ax1.legend() 29ax1.grid(alpha=0.3) 30 31# 2. 绘制MDS降维后的2维数据(右侧子图) 32ax2 = fig.add_subplot(122) 33# 同样按聚类绘制,保持颜色和标记与3D图一致 34scatter1_low = ax2.scatter( 35 low_dim_data[labels==0, 0], low_dim_data[labels==0, 1], 36 c='red', marker='o', s=50, label='聚类1', alpha=0.7 37) 38scatter2_low = ax2.scatter( 39 low_dim_data[labels==1, 0], low_dim_data[labels==1, 1], 40 c='blue', marker='s', s=50, label='聚类2', alpha=0.7 41) 42scatter3_low = ax2.scatter( 43 low_dim_data[labels==2, 0], low_dim_data[labels==2, 1], 44 c='green', marker='^', s=50, label='聚类3', alpha=0.7 45) 46# 设置2D图标签和标题 47ax2.set_xlabel('MDS降维特征1', fontsize=12) 48ax2.set_ylabel('MDS降维特征2', fontsize=12) 49ax2.set_title(f'MDS降维后2维数据结构(距离相关系数:{distance_corr:.4f})', fontsize=14, pad=20) 50ax2.legend() 51ax2.grid(alpha=0.3) 52 53# 调整子图间距,保存图片(可直接插入CSDN推文) 54plt.tight_layout() 55plt.savefig('mds_dimension_reduction.png', dpi=300, bbox_inches='tight') 56plt.show() 57
5. 额外验证:降维前后 “样本对距离” 对比
随机选取 5 对样本,对比它们在高维空间和低维空间的距离,进一步验证 MDS “保留距离” 的效果:
1# 随机选取5对不同聚类的样本(避免同一聚类内距离过近,对比更明显) 2np.random.seed(42) 3sample_pairs = [ 4 (np.random.choice(np.where(labels==0)[0]), np.random.choice(np.where(labels==1)[0])), # 聚类1-2 5 (np.random.choice(np.where(labels==0)[0]), np.random.choice(np.where(labels==2)[0])), # 聚类1-3 6 (np.random.choice(np.where(labels==1)[0]), np.random.choice(np.where(labels==2)[0])), # 聚类2-3 7 (np.random.choice(np.where(labels==0)[0]), np.random.choice(np.where(labels==0)[0])), # 聚类1-1 8 (np.random.choice(np.where(labels==1)[0]), np.random.choice(np.where(labels==1)[0])) # 聚类2-2 9] 10 11# 打印5对样本的距离对比 12print("\n" + "="*60) 13print("MDS降维前后样本对距离对比(验证距离保留效果)") 14print("="*60) 15print(f"{'样本对(聚类)':<20} {'高维距离':<15} {'低维距离':<15} {'距离误差率':<10}") 16print("-"*60) 17for i, (idx1, idx2) in enumerate(sample_pairs, 1): 18 # 确定样本对所属聚类 19 cluster_pair = f"{labels[idx1] + 1}-{labels[idx2] + 1}" 20 # 高维距离和低维距离 21 high_dist = high_dim_dist[idx1, idx2] 22 low_dist = low_dim_dist[idx1, idx2] 23 # 计算误差率(绝对值) 24 error_rate = abs(high_dist - low_dist) / high_dist * 100 if high_dist != 0 else 0 25 # 打印结果 26 print(f"样本对{i}(聚类{cluster_pair}){'':<8} {high_dist:.4f} {'':<7} {low_dist:.4f} {'':<7} {error_rate:.2f}%") 27print("="*60) 28
三、代码使用说明与结果解读
1. 代码适配性
- 若需处理自己的高维数据(如 10 维、100 维),只需替换
high_dim_data为你的数据集(形状为 [样本数,高维维度]),无需修改其他核心逻辑; - 若不想预计算距离矩阵,可将
MDS的dissimilarity参数改为'euclidean'(默认值),直接传入高维数据high_dim_data,MDS 会自动计算欧式距离。
2. 关键结果解读
- 距离相关系数:代码中计算的 “高维与低维距离矩阵相关系数” 通常在 0.95 以上,说明 MDS 很好地保留了原始数据的距离结构 —— 这是 MDS 的核心目标;
- 可视化对比:3D 图中 3 个清晰分离的聚类,在 2D 图中仍保持分离状态,且聚类间的相对位置一致(如聚类 1 与聚类 2 在高维中距离最远,降维后仍最远),证明降维未丢失关键结构;
- 样本对距离对比:随机选取的样本对在降维前后的距离误差率通常低于 5%,进一步验证 MDS “距离保留” 的有效性。
《【机器学习入门】8.1 降维的概念和意义:一文读懂降维的概念与意义 —— 从 “维度灾难” 到低维嵌入》 是转载文章,点击查看原文。


